xihuπ

【从0.99999……谈起】

这个等于1的循环小数提到过很多次了，并不是老生常谈，没得可说了。而是数学的魅力就在于此，任何一个小小的点，深挖下去，都有无穷无尽的秘密。

一些朋友在“证明”0.999……和1相等的时候，给出了这样解释。

∵0.3333…… =1/3

∴3×0.3333……=0.9999……=3×1/3=1


当然，这个问题算不上一个证明，但是是一个值得鼓励的思路，因为聪明的孩子想到了用已知的结论解决新的问题。

但是，这个解释依然不够“本质”。1/9=0.1111……  显然比1/3更为基础。


1就是这么一个无比简单却又无比深刻的数字。

比如很多人知道“1”有这样的性质：

1^2=1
11^2=121
111^2=12321
1111^2=1234321
……

111 111 111^2=12345678987654321

这样的现象，在数学上称之为数字宝塔。

 

什么？你早就知道了？

你总是这样容易被满足，于是你根本发现不了更多的秘密。 别着急，你才刚刚上路，我们先换个话题。

【缺8数的秘密】

自然数的秘密，普及的最好的，大概就是“缺8数”了吧。 这个神奇的性质，是我国当代著名数学家也是科普教育家谈祥柏先生发现的。 向前辈致以深深的敬意。

拿起你的计算器~

012345679  仔细一看，这个数字非常有规律，但是少了一个数字“8”，因此被称为“缺8数”。

缺8数最基本的性质在于，如果这个数字乘以9的倍数，他会立刻变成“清一色”的样子。

012345679×9 =111 111 111
012345679×18=222 222 222
012345679×27=333 333 333
……
012345679×81=999 999 999

当然，缺8数如果乘以3的倍数，虽然没有呈现出清一色之美，但也会出现非常规律的周期性排列

012345679×3 =037 037 037
012345679×12=148 148 148

如果你有好奇心的话，你应该问我两个问题：

①为什么会这样？

②你这一段，和上一楼有什么关系？

【数字宝塔的破坏与再生】

我第一段提到若干个1的平方，会形成一个数字宝塔。 然而，这个宝塔的完美形态，只能再111 111 111 （9个1）以下得到保持，为12345678987654321

如果1的个数继续增加，宝塔将变的面目全非。

山重水复疑无路，柳暗花明又一村。 很多时候，如果做得极端一点，可能就会毛瑟顿开，大彻大悟。

【如果无穷个1组成的数字做平方，又会是什么样的光景？】

0.1111……=1/9

(0.1111……)^2=1/81

1/81=0.012345679 012345679 012345679 012345679……

看出来了么？“ 缺8数”012345679, 正是1/81这个循环小数的循环节！

现在你明白，为什么这个数字为什么和9这么亲了吗？

【37的神秘咒语】

37是一个富有魔力的数字，但实际上，它的神奇之处远远不止于此。

37虽然是一个特立独行的质数，你似乎很难想象那些数字能被37整除。 但实际上，如果你有一个如下图所示的计算器，你立刻可以找到一大堆能被37整除的数字。

 

计算器上的怪圈：

在计算器上，1~9数字组成的九宫格中，随便一个数字开始，画一个仅有6个数字组成的圈，那么这串数字就是37的倍数。

你比如，从1开始逆时针画个圈圈，123654.（ 注意，计算器上3和6相邻，而不是3和4相邻）

123654÷37=3342
236541÷37=6393
365412÷37=9876
654123÷37=17679
541236÷37=14628
412365÷37=11145

最下面的6个数字，逆时针旋转排列，都是37的倍数。 其实，顺时针旋转排列也照样成立。

456321÷37=12333
563214÷37=15222
632145÷37=17085
321456÷37=8688
214563÷37=5799
145632÷37=3936


这才6个数字吧？ 实际上计算器能组成圈的数字多了

比如上面的6个数字：456987  不论从谁开始，顺时针，逆时针转，都是37的倍数。

比如左面的6个数字：147852  不论从谁开始，顺时针，逆时针，都是37的整数倍。

比如右面的6个数字：852369  不论从谁开始，顺时针，逆时针，都是37的整数倍。

还可以隔海向往呢！

比如最上面的3个数字和最下面的3个数字，123987，不论从谁开始，不论什么方向，都是37的整数倍。

比如最左面的3个数字和最右面的3个数字，147963，不论从谁开始，不论什么方向，都是37的整数倍。

【循环小数里的秘密】

为什么会这样？整除性与循环小数之间有着密切的联系。光一个循环小数，就足以吸引很多人倾一世情思了。

你虽然不一定能了解37为什么如此神奇，但是一看循环小数，立刻发现了37是个基佬。它在搞gay。

1/37=0.027 027 027 027……

1/27=0.037 037 037 037……


咦？缺8数012345679×3，等于什么来着？

【关于“缺8数”与37】

以上神奇的性质，都是谈祥柏先杀发现的。我一直视这位先杀为自己未曾谋面的导师，他的每一部著作我都看了好几遍。

深深被老人家对数学的热爱而打动，也对老先生对数字的敏锐洞察力佩服不已。

 
“缺8数”已经算是普及程度很高的趣味数学了，但实际上程度远远不够。比如你们可以百度百科一下“缺8数”，你会发现里面陈列的性质真不过是冰山一角。

实际上，数学历来都不缺少发现，而真正缺少的，是这些美妙发现的传播。无疑，这种神奇的感觉，很容易激发初学数学的人的兴趣。相比于枯燥乏味的三角，几何，代数，也许有趣的数字性质，更适合培养一个孩子对于数学的热情。

数字，的确是最美的数学。 它看似无比简单，却很可能蕴藏着这个世界最为深刻的道理。

不信？容我再举一个例子。

①埃及金字塔：



金字塔的几何形状有五个面，八个边，总数为十三个层面。由任何一边看入去，都可以看到三个层面。金字塔的长度为5813寸（5-8-13），而高底和底面百分比率是0．618，那即是上述神秘数字的任何两个连续的比率。

②巴特农神庙

 
③达·芬奇密码

 
④从生物，到飓风，到星云

  

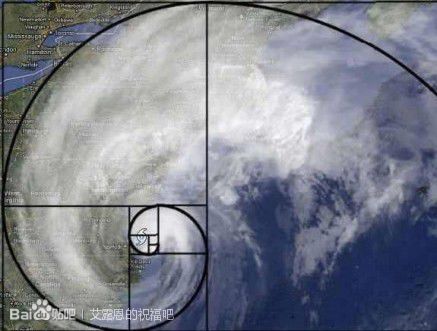
你们知道我想说什么了吗？

毕达哥拉斯：万物皆数。

这个世界最美的东西，都蕴含在这个数字里：0.618

⑤五角星。

可以查证，五角星是出现在国旗上最多的图案。 并不是因为这个图形高度对称，因为圆显然比它更对称。

人们之所以钟爱五角星，是因为这个图形里面，到处都是黄金分割。堪称最美最和谐的图案。

  

⑥世界上最重视设计与美的公司

这个Logo里面到处都是黄金分割。

 

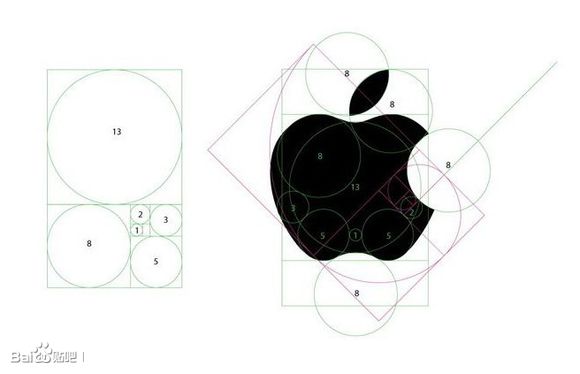
竟然还有人说三星手机好看，真是一个不可思议的事情。公众的审美水平确实亟待提高，塑料玩具怎么能和好看联系在一起呢？

我并不是一个三星黑，比如我的笔记本就是三星的，也有不少三星的小电子产品。客观来说，用起来还是凑合的。但是设计上，就是塑料玩具嘛，三星电子产品无一例外可以用4个字概括：丑的要死。

【黄金分割与斐波那契数列】

1,1,2,3,5,8,13,21,34,55,89……

我曾长期用112358作为游戏仓库的密码，或者什么东西的密码。

这个数列，就是大名鼎鼎的斐波那契数列。前两项都是1，之后每一项都等于前两项的和。

相邻两项之比，前一项比后一项，都是0.618的近似数。后一项与前一项的比值，等于1.618，恰好又是0.618的倒数。2/3,3/5,5/8,8/13,13/21… 无限趋近于黄金分割率。

斐波那契螺旋（黄金分割曲线）的画法，实际上非常简单，就是基于112358这个简单数列做的。

 
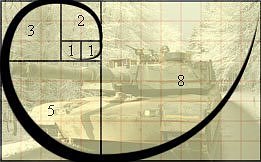
【黄金分割率的多种数学表述】

  
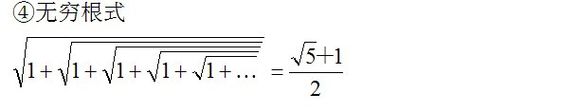
其实我个人非常喜欢最后两个算式。

体现了一种哲学思想：道生一，一生二，二生三，三生万物。

 

不过，如果就拿这些糊弄你们，怎么能体现出【自然数】的神奇呢？

【黄金分割，就在一个自然数里面！】

众所周知，黄金分割比，实际上一个无理数。

但这个无理数派生出来的菲波那切数列，竟然每一项都是自然数，而且蕴含着无数说不太清楚的自然秘密。

无理数和自然数，到底是什么关系？ 你也许想不到，这个黄金分割比，就存在于一个自然数中！

1,1,2,3,5,8,13,21,34,55,【89】,144,233，377,610,987,1597,2584,4181,6765,10946,17711,28657,46368,75025,121393……

差不多了。

我加粗了一个【89】，它又是一个质素，但这个质素，可来头不小。

1/89=0.011235 9550561797752808 9887640449438202247191

有点吓人是吧，没错，这个数字比起7,37这些，确实太吓人了了。以上那么长一串，我也没数多少位，就是它的一个循环节。

但是这个循环节虽然外表恐怖，不过异常亲切，你可以看前几位，是不就是和斐波那契数列是一样的？

（画外音：你这个也太牵强了吧。。5后面就是9，再往后乱七八糟，你这个说法无法让人信服。）

真的很牵强吗？ 人类使用的计数方式，是十进制的。 因此由于数值的限制，会出现进位现象。这导致一些真相被雪藏了，如果抛开禁止不管，你立刻会感到震惊的。

 
每一个加数，都是斐波那契数列中的一项

结果，就是1/89


这个神奇的无理数——黄金分割比，就这么的雪藏在了89这个自然数里面。

【后记：数论的魅力与意义】

我举了一些例子，很多都是你们百度找不来的。实际上这就是“数”的魅力。它是如此的神奇，以至于多少人一接触，就再也放不下了。

自然数里的秘密，真的是无穷无尽。而似乎，真理又总是存在于这些最朴素的数字里。 每一个数字的秘密，都能写一篇论文，甚至是一本书。


为什么所有大数学家，无一例外的都要研究数论？

不仅仅是因为它的神奇让人着迷，实际上，研究数论有着非常深刻的学术意义。

①你们现在学的范围最大的数，叫做复数。复数被定义为a+bi

你可以清楚的看到，复数本质上是有（a,b)这样一个有序实数对定义的。换言之，只要实数的性质研究清楚了，复数的性质自然就清楚了。

②实数，初中生都知道，由无理数和有理数组成。现代数学把实数定义为“对有理数的分割” 你们都知道有理数并不是连续的，它们中间存在大量的空隙，这些空隙被无理数占据着。

想象把所有的有理数看做一串点，按顺序排成队，它们并不是一个挨着一个，中间存在着空隙。用一把刀砍下去，如果砍到东西了，说明你砍到的是有理数；如果一刀砍空了，说明你砍到的是无理数。

现代数学就是这么定义实数的：实数，是对有理数的一种分割。

换言之，实数是由有理数定义的。只要有理数的性质清楚了，实数的性质自然就清楚了。

③有理数，被定义为两个整数的比值。

简而言之，只要整数的性质清楚了，有理数的性质就清楚了。

④整数包括正数，负数，0. 负整数完全由正整数定义，0和正整数统称自然数。

也就是说，如果自然数的性质研究清楚了，整数的性质就全清楚了！


我们倒过来看：

清楚了自然数，就清楚了整数；
清楚了整数，就清楚了有理数；
清楚了有理数，就清楚了实数；
清楚了实数，就清楚了复数。

你们现在知道，数论的地位了吗？

【人类，离数字的秘密，只有一步之遥】

自然数，还能不能继续划归呢？

0和1是非常特殊的两个自然数，在代数群论里，作为零元和幺元出现。 （当然0和1不一定就是0是0元，1是幺元，这取决于定义了什么样的运算，有兴趣的可以找一些群论的著作来读，我曾经给你们介绍过它的创始人：伽罗华）


剩下的自然数，可以被分为质数和合数。 只能被1和自己的整除的数，被称为质数。

合数，能不能由质数来定义呢？

数论基本定理告诉你们：任何一个合数，都可以分解为若干个质数的乘积，且只有一种分解方法。 小学生都会的“质因数分解”，实际上，如果能把一个数分解成质因数，这个数字的性质也就清楚了。

你比如我上次写的520,1314的问题。实际上全部秘密，都在于我研究了1314最关键的一个质因子73的循环节。

但是，这个定理是不能让人满意的。 因为一个大数，分解它的质因数实际上是困难的，而且，分解了研究起来也很不方便。 你比如100万个质数乘起来得到一个合数，就算你有能力分解它，那你得到100万个质因子，这怎么研究呢？

【数学皇冠上的明珠：哥德巴赫猜想】

欧拉是公认的，有史以来解决数学难题最多的数学家。欧拉在世的时候，全世界所有科学家都尊奉其为自己的老师。 当时世界学术界有一个传统，谁有不会的题，都会给欧拉写信，过几天，就会收到正确的答案。

欧拉也是有史以来公认的，心算能力最强的人。他心算的不是一般“小神童”的加减乘除，而是复杂的高等数学，与逻辑推理。

这是因为，欧拉晚年双目失明。 你想象一下如果你看不见，你连算三位数乘法都有困难，还怎么研究数学呢？ 某种意义上说，眼睛对数学家的重要程度，不低于耳朵对音乐家的重要程度。 然而，欧拉失明一直到他去世的17年间，他依然凭借无与伦比的记忆力与心酸能力坚持科研，发表大师级论文400多篇，回答世界各路人士提问不计其数。

很多人认为，如果欧拉眼睛没坏，那么哥德巴赫猜想，就留不到今天了。

 

1742年，哥德巴赫给欧拉写了一封信。他提出了一个猜想，大致意思（我表述的不严密，但是为了让你们理解内涵），所有整数都可以表示为3个质数的和。

【欧拉被难住了】

虽然欧拉当时只是一只眼睛失明，另一只眼睛勉强看得见。但是，他依然没有解决这个问题。

他给哥德巴赫回信说：这个猜想意义深远，非常的伟大，它很可能是正确的，但我一时找不到好的证明。 不过，我提出了它的一个等价命题：

任何一个大于2的偶数，都可以表示为2个质数之和。

我们现在提到的哥德巴赫猜想，都是欧拉的这种表述。

我必须在这里郑重强调：哥达巴赫猜想是一个意义深远，伟大而又严肃的命题。

这个命题和1+1=2没有半毛线关系。也不知道谁说的，哥德巴赫猜想就是证明1+1=2，这种说法以讹传讹，导致歌猜在中国尽人皆知。但竟然是这样一种荒谬的科普方式，不禁让人感到汗颜。

比如
4=2+2
6=3+3
8=3+5
10=3+7
12=5+7
14=11+3
16=13+3
18=13+5
20=13+7

……

不用试了，自从有计算机以来，世界上运算速度最快的计算机，一直在用穷举法验证哥德巴赫猜想。可以这么说，迄今为止，人类能发现的大偶数，无一例外符合这个猜想。

哥德巴赫猜想看起来是那样的正确，可是，快300年过去了，谁也证明不了。

【哥德巴赫猜想】与“a+b”和“1+b”的证明方法

哥达巴赫猜想是意义深远的，如果能把任意一个整数分解成3个质数之和，这无疑相当于宣告：整数的问题可以划归为0,1和质数的问题。

于是但凡研究数学的人，无疑不对这个未解难题垂涎三尺。 你包括我，最近阅读的材料都是王元，陈景润，华罗庚的关于这个猜想的研究成果。

当然我不说大话，只不过是作为一种兴趣爱好，了解一下这个问题罢了，你们不要想太多。万一哪天一不小心，对吧……

实际上,在中国广为流传的“1+2”和“1+1”，说的不过是哥德巴赫猜想的一种证明方法罢了。

这个猜想最大的难点在于，一般无穷的问题，我们只能用归纳法或者反证法解决。

但是质数的生成是没有递推规律的（或者更严格的说，是人类尚未发现质素之间的递推关系），导致归纳法用起来非常困难。

于是一些科学家尝试，能不能用逼近的方法接近哥德巴赫猜想？也就是先证明一些要求宽松的命题，从中探寻规律再利用这些规律证明猜想。 这实际上也符合人类解决问题的一般思路，由浅入深，由简单到复杂，由特殊到一般。

【“a+b”证明方法】

法国人提出来的，他提供了一种思路，我们可以先放宽要求，把问题改成：

任何一个大于2的偶数，都可以表示成【两个部分】的合

这两个部分，每一个部分都可以被表示为【有限个质数的乘积】，其中一个部分可以表示成a个质数的乘积，另一个部分可以表示为b个质数的乘积。

这个命题就被称为“a+b”命题，而哥德巴赫猜想，按照这个定义，实际上就是要证明大偶数可以被表示为“1+1”的形式。

注意：这个1+1的意思是，偶数可以表示为两个部分的和，每一个部分都是1个质数。这和“1+1=2”显然没有半毛线关系。

法国人率先证明了“9+9”，

即一个大偶数，都可以表示为两部分的和，每一个部分都可以表示为9个质数的成绩。

实际上，a+b两部分，都是合数。这和哥德巴赫猜想本质上完全不同。

随后，中国数学家在这个问题上取得重大突破，从9+9出发，连续减少a和b的数字。 王元院士在这个问题上攻城拔寨，一直把“9+9”减小为“1+3”。中国科学家证明用到的思路是“筛选法”，其实，到1+3，已经非常艰难了，当时普遍认为这个思路已经走投无路了。

1966年，王元先生的师弟，在中国尽人皆知的数学家陈景润先生，发表了论文《表达偶数为一个素数及一个不超过两个素数的乘积之和》，震惊世界。 陈景润用非常巧妙的方法，证明了“1+2”。 看似一小步，实际上真的是困难重重，陈景润先生，已经把筛法用到淋漓尽致了，换句话说，筛选法，已经走山穷水尽了。

【一步之遥还是咫尺天涯？】

很多科普杂志或者媒体，经常说陈景润把哥德巴赫猜想证明的只有一步之遥。实际上这种说法非常不负责任。

哥德巴赫猜想：

任何一个大偶数，都可以表示为两个质数的和。  关键在于，它的落脚点是2个【质数】


“a+b”证法，本质上是研究2个【合数】的关系。

“1+b”证法，本质上是研究1个【质数】和1个【合数】的关系。


而“a+b”与“1+b”中的合数，要想划归为质数，何尝不是“哥德巴赫猜想”呢？

这种证明方法，无异于用“0.3333……=1/3”来证明“0.9999……=1”，你没有解释,0.3333……为什么等于1， 这个证明就是无效的。


“a+b”证法，终点就是“1+2”，这个方法永远到不了“1+1”。看似一步之遥，实则咫尺天涯。

就好像小孩子玩拼图，每次都只有最后一块放不上去，但这说明，你前面所有的努力，都是错误的。必须拆了重来。

并不是否认陈景润先生的功绩，陈先生的地位历史早有定论，拜读陈先生的著作，深感其治学严谨，思路活跃，特别是对筛法的使用，估计前无古人后无来者了。 而且陈景润证明的“1+2”，本身也是一个非常伟大的定理了。

我只是想说明：要想真的证明歌猜，必须找到完全创新的一个思路。 传统方法，都已经强弩之末，无力回天了。

【最后补充上我在另一个帖子里关于7的叙述】

一：我和幸运数字7

 
很多人的幸运数字似乎都是7，因为扔两个骰子似乎很容易得到这个数字。

上了中学，学了点简单的概率知识后，你会发现其实并不是你和7有缘，而是两个骰子扔出7的概率是最高的。

比如我和别人就不一样，一般人喜欢数字6，8 ，9；而我却钟爱7。很多人认为这和我喜欢一本叫《鹿鼎记》的名著有关，其实这是一种误会。 我喜爱7，是因为我很早就发现这个数字是那么的与众不同。


 
我小的时候，同龄人一般喜欢这么几种玩具：恐龙模型，变形金刚，玩具气枪，四驱车等等。

而我总觉得这些玩意没什么意思，特别是一个小孩追着四驱车炮，配着“biu biu du du da da”的声音玩玩具枪，感觉特别傻。 所以说心理年龄超越同龄人十几岁是个很痛苦的事情，总是那么的缺乏童趣。

而我对七巧板，九连环，孔明锁之类的东西情有独钟。尤其对算盘这个东西爱不释手。我们小时候会学习珠算的，那时候爸爸给我买了一个10档玩具算盘。

我很认真地告诉他：这个不行，太小了，算不了开方。于是我父亲非常吃惊，算盘可以开方？ 我说当然，于是我就在一个10档小算盘上开了一个根号2。

你可以想象，一个刚学了九九表的三年级学生竟然已经知道了无理数这种东西，并且能用算盘完成精确计算，这是一个很不可思议的事情。于是我父亲立刻出去买了当时能买到的最大的算盘：一个48档的算盘。

由于从小对这个东西非常的亲切，以至于经常表现出异于常人的计算天赋。有人问我你怎么算的这么快，我很扭捏，羞涩地告诉他们：我也不知道啊，好像是与生俱来的。于是四下里惊呼天才神童乱七八糟的。

长大了，我觉得这样不好，因为这是骗人的，现在也应该把这些秘密说出来了。实际上是因为我家有一本旧书，民国版的《直指算法综统》，这是明朝数学家程大位先生所著的“珠算百科全书”。

这应该是中国古代最伟大的数学著作了，如果把数学分为《几何》与《算数》，那么来自古希腊欧几里得的《几何原本》代表着几何的最高水平；那么来自中国的《算法综统》，就应该是算数的登峰造极之作。

十几岁的时候虽然不能完全认识上面写的繁体字，但是简单的口诀，丰富的图示，加上算盘不离手的勤奋练习，还是很快掌握了很多高超的珠算算法。现在据说有一门社会培训被称之为《珠心算》，神乎其技，吹的天花乱坠。 我一看他们的教材，便知道这东西滥觞于《算法综统》，早在400年前就很成熟了。

我们小时候流行武侠小说，好像很多主角都无意中捡到一本秘籍，结果主角还不识字，开着图玩了两天就练成绝世神功。实际上我对珠算就有这种感觉。遗憾的事情在于，《算法综统》自民国以后，似乎没有再版，这是一件很遗憾的事情。反观《几何原本》，其发行量与流传程度，仅次于《圣经》。

说了这么多，为什么说我和7有缘？ 因为算盘一档上，挂着7个珠子。

7这个数字真的是非常的神奇，不过似乎只有懂它的人才能懂得它为什么如此的神奇。

你比如说，7虽然是个特立独行的质数，只能被1和它本身整除。

❤①：7包含在所有“吉利数字”之中

但如果把它作为除数，它竟然能整除掉所有的吉利数字。你比如666666，你比如888888，你比如686868，你比如668668，再比如886886. 这些数字竟然都是7的整数倍。


❤②：最独特的循环小数

1/7=0.142857 142857 142857……

大家可能对1/3=0.3333…… 1/9=0.1111……比较熟悉。并且基于此能能提出“0.9999……为什么等于1”这样的高端问题。

但显然，1/7的样子就有点吓人了。7是如此简单的一个数字，而它竟然拥有着6位循环节。但你也许不知道的是，这循环节里的6位数字，竟然隐藏着无数惊天的秘密。


142857是我的银行卡密码，你们怎么懂我的情怀呢。

★不可思议

142857×2=285714
142857×3=428571
142857×4=571428
142857×5=714285
142857×6=857142

看出什么了吗？多么的不可思议，不论乘以几，结果只不过是原来的6个数字颠倒顺序罢了。

★真的很不可思议

142857×7=999999


★这才是不可思议的事情

众所周知，5个点可以确定一个二次曲线。 就好像2点能确定一条直线，不共线的3点能确定一个圆一样。

6个点能在一个圆锥曲线上，是一种缘分；如果6个点竟然公椭圆，并且还存在3线共点，那就非常的不可思议了。

142857按照相邻关系，可以形成这样6个点。（1,4）（4,2）（2,8）（8，5）（5,7）（7,1） 之后就开始重复循环了。

这6个点竟然在一个椭圆上！ 而且存在三线共点的“巧合”

 
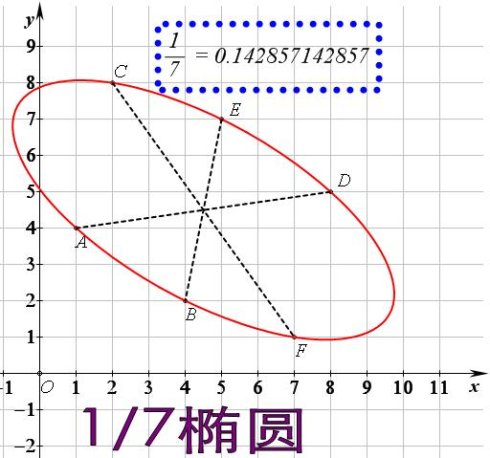
（注：这个事情不是我发现的，是偶然拜读彭翕成老师的文章学习到的）


❤③ 7与数学家的故事

很多数学家都和7这个数字有缘。


【高斯与“七等分圆难题”】

比如德国数学王子高斯，19岁时证明了争论2000多年的尺规作图难题“七等分圆是无法用尺规实现的”。 高斯实际上解决了所有圆的等分问题，比如虽然“七等分圆”不能实现，但是“十七等分圆”确实可以的。

这个证明是高斯的成名之作，他本人非常得意，生前希望在自己的墓碑上刻一个正十七边形。但高斯去世后，工匠认为这个正十七边形太丑了，因为它很像一个画的很蹩脚的圆，所以工匠把它改成了“正十七角星”刻在了高斯的墓碑上。

 
 
【欧拉与“哥尼斯堡的七座桥”】

 

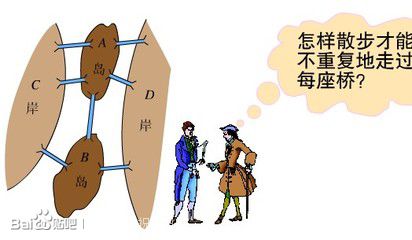
这个问题讲过了，这里不再重复。29岁的欧拉，实际上一劳永逸的解决了“一笔画”问题，并由此开创了现代数学中炙手可热的《图论》分支。

【高斯的不朽著作《算术研究》，共有7个章节】 （我有这本书的英文版，如果你们谁兴趣浓厚，并且我认为你有能力读这本书，我可以借给你看。这真是本惊世之作）

【祖冲之用割圆术，把圆周率π计算到了小数点后的第七位】

 

【七巧板被誉为这个世界最神器的玩具，看着就7个部分，已经拼出2000多种图案了】

七巧板早在几百年前，已经能拼出千人千面的108种人物了。各种形态，能反映人物的性格与活动，非常神奇，所以什么样的玩具培养什么样智商的孩子。 现在的小孩都玩装帧精美价格不菲的“喜洋洋与灰太狼”拼图，难怪孩子越来越傻。


【你知道数学学术界最著名的著作共有几本？】 数学七大名著！

1 《从微分观点看拓扑》J.W.米尔诺 　　
2 《 无穷小分析引论》 Introduction to analysis of the infinite 欧拉 　　
3 《自然哲学之数学原理》 伊萨克.牛顿 　　
4 《几何原本》 欧几里得　　　
5 《数论报告》希尔伯特 　　
6 《算术研究》高斯 　　
7 《代数几何原理》哈里斯（Harris）
 
上图为欧拉的著作《无穷小分析引论》。关于欧拉，我赞美的太多了。

不如听一听另一位伟大的数学家，拿破仑的帝师，数学分析大师拉普拉斯对欧拉的评价

Read Euler, read Euler, he is the master of us all！ （读读欧拉，读读欧拉，他是我们所有人的老师！）
 

不信？你知道多面体的性质：

定点数+面数-棱数=2 是谁发现的吗？

牛顿一生算不出来的月球“跃动”问题，双目失明的欧拉心算几天就搞定了！

指数，三角函数，复数，自然对数的底数e，完全是在不同领域内单独定义的。本来各不相干，井水不犯河水，他们各自独立的发展了千百年。 可想而知，当欧拉写出这个公式的时候，当时的人们该有多么吃惊！

 
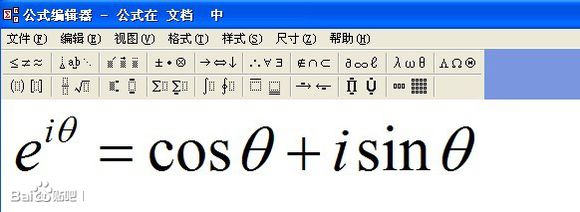
物理学家一直认为，万有引力，静电力，磁力在表达式上是如此的相似，以至于他们非常愿意相信这些场力本质上是一种力，于是有着寻找磁单极子的百年尝试，可惜一直缺乏有力的实验证据。  

然而，欧拉发现的欧拉公式，实际上相当于把以前毫不相干的几个数学分支彻底的统一了起来，他在数学领域，实现了类似于物理学家们一直追求的梦想。

PS：

不过我并不建议你们读这几本书，大师的学术作品需要很深的功底才能接受，包括我，作为一个普通爱好者，只能粗浅的从这几本书中感受一下大师风范罢了。

这里面唯一有可能被初学者深刻理解的，就是《几何原本》了。不过如果你们想看数学书，我倒是可以推荐很多有趣的书给你。